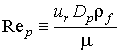
|
流体中の粒子・気泡の運動 |
粒子の受ける流体抵抗
流体中を運動する粒子に関するRe数は、流体と粒子の相対速度urを代表速度に、粒子径Dpを代表長さにとり、流体の密度ρf、流体の粘性係数μとから次式で定義される。
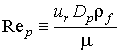
流体中の物体が流体と相対運動をする場合、物体は形状による抵抗と流体の粘性によって流れの方向に抵抗力FD
[N](抗力 drag force)を受ける。
物体の投影面積Ap
あたりの抗力を対流による運動エネルギーで無次元化して抵抗係数CD :
![]() (球の場合は
(球の場合は![]() )
)
を定義する。Re
とCD の関係が示されれば、それはスケールを問わない関係となる。
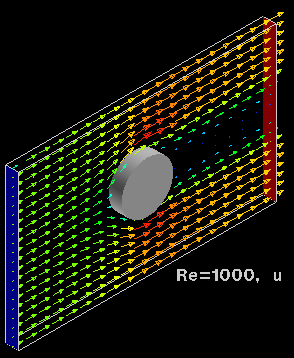
抗力は物体表面のせん断応力の流れ方向の積分値である摩擦抵抗(friction drag, skin drag)と物体表面の圧力の流れ方向の積分値である圧力抵抗(pressure drag)(形状抵抗(form drag))に分けることができる。一般にReの小さい範囲では摩擦抵抗の割合が大きくReが大きくなると形状抵抗が支配的となる。
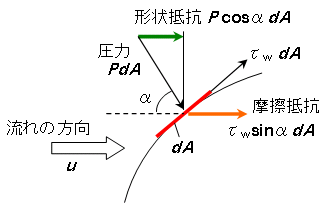
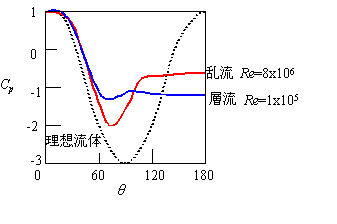
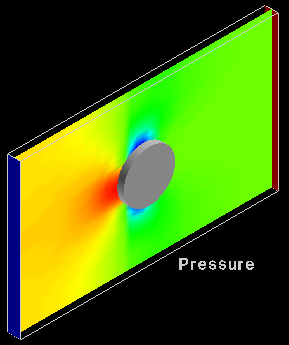
このうち圧力抵抗の例を円柱についてみてみる。図は流れ中の円柱周りの圧力分布を圧力抵抗の係数であるCp:
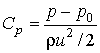
で示したもの。Pが角度θ位置における円柱表面の圧力、
p0は無限遠における圧力である。既述のように粘性を考えない理想流体(流速が無限小)ではsin曲線で与えられる。
![]()
この場合圧力分布が前後で対称なので、円柱に圧力は働かず、さらに粘性力も無限小なので、圧力抵抗、摩擦抵抗ともの0となり、円柱に抗力が働かないことになる。(ダランベールの背理)流速が大きくなると、θ=70度で最小圧力となり、その後境界層がはく離し、その後方は一定の圧力となっている。乱流の場合ははく離点が後方に移り、はく離域の圧力が大きく、抵抗力は小さくなる。これらのことは球の場合も同様である。
球のまわりの遅い流れ
遅い流れ(Re<<1)ではナビエ−ストークス式の慣性項が粘性項に比較して省略でき、次式となる。
![]()
![]()
![]()
この式を球の表面上で速度0の条件で解く。その解法はストークスStokesによってなされた。(1851)その誘導はむずかしいので、結果を示すと次式となる。
![]()
![]()
(ただし、![]() ,a
:球の半径, ur:流れの速度, 流れの方向をx方向とし、原点を球の中心とする。)これを球の中心からの距離rとx軸となす角度θにより表すと次式となる。
,a
:球の半径, ur:流れの速度, 流れの方向をx方向とし、原点を球の中心とする。)これを球の中心からの距離rとx軸となす角度θにより表すと次式となる。
![]()
![]()
![]()
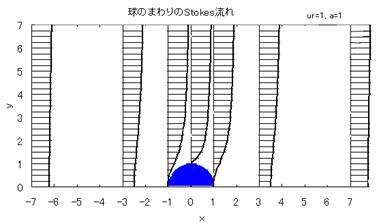
速度分布(u)を図に示す。流れは球の前後で対象である。ストークスの解では流速分布はレイノルズ数Reも粘性係数μも無関係である。
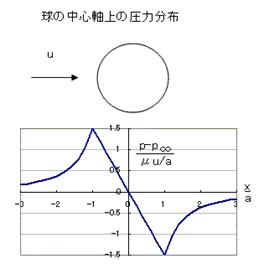 この結果をもとに流れ中の球に働く力を考える。この解によると、球の中心軸上の圧力分布は図のようになっている。球の表面に働く圧力の分布は
この結果をもとに流れ中の球に働く力を考える。この解によると、球の中心軸上の圧力分布は図のようになっている。球の表面に働く圧力の分布は
![]()
であり、最大圧力と最小圧力は球の前端と後端に生じている。
![]()
また、球表面に働くせん断応力は次式で求められる。
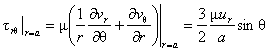
圧力のx方向成分と球表面でのせん断力のx成分を球の全表面について積分する。
![]()
ここで球表面の面要素dSは![]() なので、
なので、
![]()
となる。これによると低レイノルズ数での流体中の球におよぼされる抵抗は2/3がせん断力(流体摩擦)によるものであり、1/3が圧力によるものである。またFDは流速に比例し、球の質量とは関係がないことが特徴である。
結局、球に働く抗力を抵抗係数CDであらわすと次式となる。
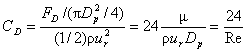
これをストークスの抵抗法則(Stokes's law of resistance, 1845)という。概略値としてはこの法則の適用範囲はRe<10まで拡大してよい。
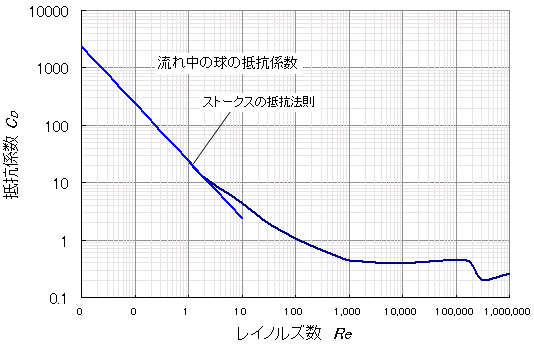
球の抵抗係数CD
の一般的関係は図のようである。Re の大きい範囲
(500<Re<105)では実験的に、
![]()
で求められ、この領域を Newton域と呼ぶ。この式にはStokes式と異なり、μの代わりに慣性に関係する流体密度ρがはいっており、慣性が抵抗を支配していると言える。
Newton域とStokes域の間
1<Rep<104は、
![]()
又は![]() の式で近似できる。
の式で近似できる。
Newton域を越えたRe>30,000になると、球、円柱ともに急激に抵抗が減少する。これは固体表面の境界層が乱流に遷移をはじめたものである。(これを利用して球表面の乱流遷移を早めてやれば低い速度域から抵抗を小さくできる。ゴルフボールがそれである。)
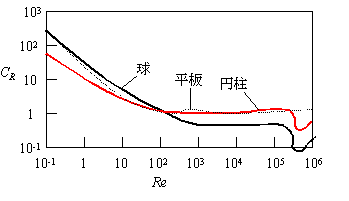
流れ中の物体が球以外でも抵抗係数は似通っており、平板、円柱について図に比較する。
重力場における球の沈降
静止流体中の質量m[kg]の球形粒子が重力により速度vで運動(沈降)することを考える。粒子の運動方程式((質量)×(加速度)=(力))は次式となる。
![]()
ここで右辺の力の項はそれぞれ重力、浮力、抵抗力を表わす。これは![]() と抵抗力の定義式より、
と抵抗力の定義式より、
![]()
となる。この式をみてわかることは、vが正であれば、時間が経過するにつれて流体抵抗をあらわす右辺第2項が大きくなり、第1項(重力と浮力の差)に近づく。例えば低Re数におけるストークスの抵抗法則CD=24/Reを代入して解くと、
![]()
の形の式となる。
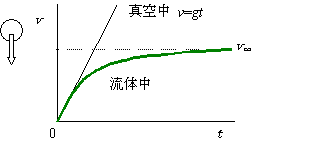
両者が等しくなると加速度は0となり、流体中の球は一定速度で等速運動をするようになる。この速度vt:
![]()
を終末速度(terminal velocity)または終末沈降速度(terminal settling velocity)という。
低Re数では、Stokesの法則におけるCDを代入して、
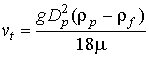
となる。この式は実用上きわめて重要な式である。粒子の沈降速度はDp2に比例する。
さらに、抵抗係数として、中間域の式およびNewton域の式を用いた場合の終末速度は次式となる。
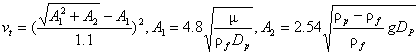 (1<Rept<104)
(1<Rept<104)
![]() (103<Rept<2×105)
(103<Rept<2×105)
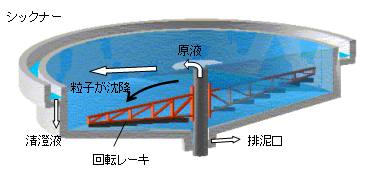
終末速度より粒子径を得ること
これらのことを利用して、測定可能な固体粒子の終末速度を測定して粒子の径を求めることができる。実際、不規則な形状の固体粒子の径を定める方法として、液中での沈降実験から終末速度を求め、これと終末速度の等しい同一密度の球の直径をこの粒子の径とする場合である。このようにして定義された径を沈降速度径といい、特にStokesの抵抗法則の成立する範囲の径をStokes径という。
遠心力場における粒子の運動
遠心力場における粒子が旋回半径r,角速度ω, 半径方向速度vrで運動しているときは、粒子に働く遠心力と流体抵抗がつりあっているので次式の関係となる。
![]()
Stokesの法則が適用できる範囲(Re<1)では、右辺が3πμvrDpなので、
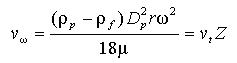
となって、遠心力場における終末速度vωは重力場における終末速度式のgを遠心加速度rω2で置き換えた式となる。重力場における終末速度との比Zを遠心効果と呼ぶ。遠心力場では粒子の沈降速度が重力場に比べてZ倍大きくなるので、細胞など流体中の微少な粒子の分離操作では遠心式の装置が用いられる。
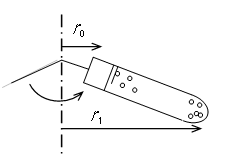 【例】発酵液とその中の酵母菌(球形と仮定、径
8 μm、密度 1050 kg/m3)を9000 rpmの遠心機により分ける。容器液面と底の回転中心軸からの距離rをおのおのr0
=0.03
m, r1=0.10 mとして、酵母を沈降分離するのに要する時間を求める。
【例】発酵液とその中の酵母菌(球形と仮定、径
8 μm、密度 1050 kg/m3)を9000 rpmの遠心機により分ける。容器液面と底の回転中心軸からの距離rをおのおのr0
=0.03
m, r1=0.10 mとして、酵母を沈降分離するのに要する時間を求める。
上式より、酵母菌の位置r に関する式が
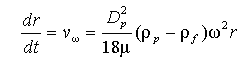
である。これを積分して、t =0でr = r0,
t =t1でr= r1とすると、
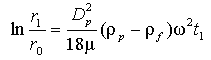
となる。従って、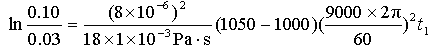
より、t1= 458 s = 7.6 min 。
気泡・液滴の抵抗係数
流体中の気泡の運動方向は上昇であるが、その運動は重力、浮力、抵抗力に支配されることは全く固体粒子と同様である。気泡及び液適の抵抗係数はReの小さい範囲では次の Hadamard-Rybczynskiの式で近似できる。
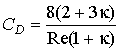
ここでκ=μ/ μ L。μは液滴または気泡の粘度で、 μLは連続相流体の粘度である。
演習
【9-1】【雨の降る速度】一気圧の空気中(密度ρf=1.205 kg/m3, 粘度μ=1.8×10-5 Pa・s)で雨が降っている。径D p =0.abc [mm]の雨滴が降ってくる速度を求めよ。雨滴をρp=1000 kg/m3の固体球形粒子として計算する。g=9.8 m/s2
【ヒント】Newton域を仮定すると、抵抗係数が、CD=0.44、なので、終末速度はvt=?となる。念のためこれからRe (=vt Dp ρf /μ)を計算すると、Re =?である。
【9-2】【気泡の上昇速度】水中を径3 mm の気泡が上昇する速度を求めよ。上の問題とρf, ρpが入れ替わる。Stokesの抵抗法則を仮定しておこなう。(この場合は初めにReを仮定してからおこなうので、求められた速度から再度Reを計算するという繰り返し計算となる。)