| プロセス流体工学 8 次元解析と無次元数 |
複雑な物理現象をより基本的な無次元数の組み合わせ として解析し、現象のスケールを問わない一般性のある結果を得るための手段が相似則(law of similarity)である。無次元数をもとに解析を進めることで実験を少なくできるし、無次元数により結果を整理することで,その結果を化学工学の主な目的であるスケールアップに利用することができる。
無次元数の代表レイノルズ数
流れの場の代表的長さ(管の径や物体の長さ)代表的速度をそれぞれl, U とする。時間の代表をを![]() 、圧力の代表を
、圧力の代表を![]() とする。これらの代表量(スケール)により長さ、速度、距離、圧力を無次元化する。(gは重力加速度)
とする。これらの代表量(スケール)により長さ、速度、距離、圧力を無次元化する。(gは重力加速度)
![]()
これらより、ナビエ-ストークスの式は次式のように無次元変数で表せる。(x方向のみ示す)
![]()
 この式は無次元だから()内の値もまた次元のない量すなわち「無次元数」であり、次のように定義される。
この式は無次元だから()内の値もまた次元のない量すなわち「無次元数」であり、次のように定義される。
レイノルズ数:![]() フルード数:
フルード数:![]()
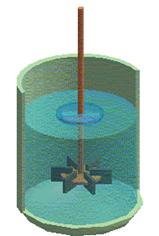
 上式は無次元であるから、このReが同じであれば流れのスケールにかかわらず流体の現象は同じであると言える。これをレイノルズの相似法則という。これにより大きいスケールの現象を小さなスケールの模型実験により推定することができる。例えば撹拌槽内の流れを考えた場合、大小の撹拌槽のフローパターンを等しくするためには Re と Fr を等しくすればよい。
(撹拌羽根の径を代表長さl とし、回転速度n とl の積を代表速度U とする。)
上式は無次元であるから、このReが同じであれば流れのスケールにかかわらず流体の現象は同じであると言える。これをレイノルズの相似法則という。これにより大きいスケールの現象を小さなスケールの模型実験により推定することができる。例えば撹拌槽内の流れを考えた場合、大小の撹拌槽のフローパターンを等しくするためには Re と Fr を等しくすればよい。
(撹拌羽根の径を代表長さl とし、回転速度n とl の積を代表速度U とする。)
また、レイノルズ数は上式の意味から慣性力(左辺)と粘性力の比と考えることもできる。
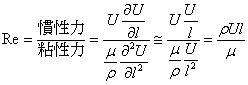
レイノルズ数が大き く慣性力が勝ると,流れ中の変動(渦)が減衰せずに流れは乱流となる。レイノルズ数が小さく,粘性力が勝ると,流れ中の変動は粘性で抑制され,流れは混合のない層流となる。
次元解析とπ定理
次元解析は「ある物理現象に関係するすべての変数物理量間に理論的な関係式が成立するものとすれば、その式は次元的に健全なものでなければなれない」という原則にもとづくもので、これにより現象に関与する多くの物理量を少数の無次元項 (dimensionless group)にまとめることができる。
ある物理現象に関係する変数物理量や次元定数(重力換算係数gcなど)をA1,A2,・・,An とし、これらの間に次のような関数関係が成立するとする。
f (A1,A2,・・,An) =0
この関係が使用する単位系にかかわらず成立するとき、その方程式を完全方程式と呼ぶ。次元解析の対象とする方程式は完全方程式でなければならない。完全方程式は、変数A1,A2,・・An のべき乗積により作られる無次元項π1,π2,・・・,πpを用いて表わしたつぎの関係式:
F (π1,π2,・・・,πp )=0
に変形でき、無次元項の数 p は、変数物理量の数 n と採用した単位系での基本量の数 m との差に等しい。これをπ定理という。
以下に 多くの教科書から次元解析の例を収集した。次元解析の方法はいくつか様式があるのだが,ここでは全て同じパターン(着目物理量を左辺に置く形式)で次元解析をおこなう。
なお,全ての例でべき数を消去する段階(「いまd を残して他をd であらわす」)が必須だが,ここで「なにを残すか」の選択は重要である。実際には残す べき数は最後の無次元数の形を見越して決めており,仮に別の べき数を選ぶと無次元数の構成に失敗する。この点が次元解析の怪しい?ところである。
数学的に根拠のある方法がなくはないようであり,最近の教科書*)には「階段行列echelon form matrix」操作(ベクトルの基底変換)により,最終的な無次元数群を解析的に決める方法 が説明されている。
*:P.A. Ramachandran: Advanced Transport Phenomena, p. 485 , Cambridge University Press (2014)
管内流れの圧力損失
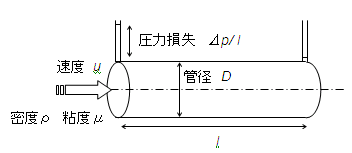 管内径D [m]の円管内を密度ρ [kg/m3]、粘度μ [kg/(m・s)]の流体が速度u
[m/s]で流れている。この4個の因子の関数として管単位長さあたりの圧力損失(Δp/
l ) [Pa/m=kg/(m2・s2)]が決まるとして、圧力損失を表す無次元式を求める。
管内径D [m]の円管内を密度ρ [kg/m3]、粘度μ [kg/(m・s)]の流体が速度u
[m/s]で流れている。この4個の因子の関数として管単位長さあたりの圧力損失(Δp/
l ) [Pa/m=kg/(m2・s2)]が決まるとして、圧力損失を表す無次元式を求める。
変数物理量の数n は5であり、基本量の数m は質量 M,長さ L,時間 Tの3。したがってπ定理によって無次元数の数 p は2であることが予測される。
圧力損失が
(Δp/ l )= k D a u bρcμd
のようにあらわせると仮定する。(k
は無次元の定数)これらの基本量も次の関係になくてはならない。
[ML-2T-2]=[L] a [LT-1]b
[ML-3]c [ML-1T-1] d
各変数間の関係が完全方程式であるためには両辺の次元が一致しなければならないから、基本量の関係式のべき数も左右で一致しなくてはならない。よって、各指数に関して、
Mに関して 1=c+d
Lに関して -2=a+b-3c-d
Tに関して -2=-b-d
が成り立つ。いまd を残して他をd であらわすと、
a =-1-d
b =2-d
c =1-d
となる。これをもとの変数間の関係式に代入すると、
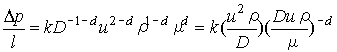
となり、これを変形して次式が得られる。
![]()
これが次元解析の結果で、ここで得られた二つの無次元数は、(ΔpD / (ρu2l )) の1/2をファニングの摩擦係数 f 、((ρuD) /μ)をレイノルズ数(Re)と呼ぶ。
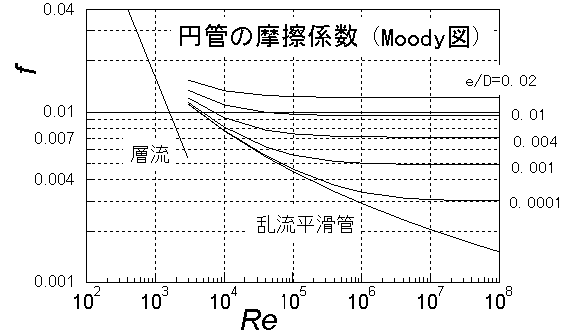
流れ中の物体に働く抗力
 投影面積A [m2]の物体が密度ρ[kg/m3]、粘度μ[kg/(m・s)]の流体中を速度u
[m/s]で動くとき、物体が流体から受ける抗力D [N=kg・m/s2]について次元解析をおこなう。
投影面積A [m2]の物体が密度ρ[kg/m3]、粘度μ[kg/(m・s)]の流体中を速度u
[m/s]で動くとき、物体が流体から受ける抗力D [N=kg・m/s2]について次元解析をおこなう。
抗力が
![]()
のようにあらわせるとする。(k は無次元の定数)すると次元間にも次の関係が成立しなくてはならない。
[MLT-2]=[LT-1]a [L2]b [ML-3]c [ML-1T-1]d
よって、
Mに関して 1=c +d
Lに関して 1= a +2b-3c-d
Tに関して -2= -a -d
いまd を残して、他をdであらわすと、 c =1-d, a =2-d, b =1-0.5d。よって、
![]()
すなわち、![]()
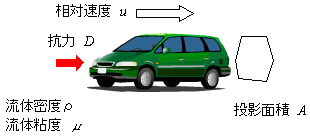
![]() である。左辺が抗力係数CDという無次元数、右辺にレイノルズ数があらわれる。よって物体の受ける抗力は抗力係数とレイノルズ数により一般的な関係として表せる。
である。左辺が抗力係数CDという無次元数、右辺にレイノルズ数があらわれる。よって物体の受ける抗力は抗力係数とレイノルズ数により一般的な関係として表せる。
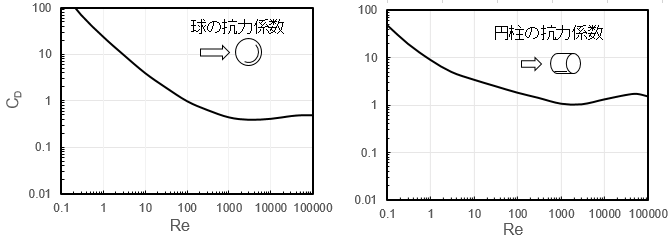
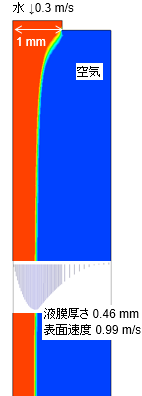
流下液膜の厚さ
 密度ρ[kg/m3],粘度μ[kg/(m
s)]の流体が壁面を単位幅当り体積流量Q[m3/(m2 s)]で流下するときの液膜厚さδ[m]について次元解析をおこなう。関係する物理量は重力加速度g[m/s2]を加えて5個である。液膜厚さδが次式のように表せるとする。(kは無次元の定数)
密度ρ[kg/m3],粘度μ[kg/(m
s)]の流体が壁面を単位幅当り体積流量Q[m3/(m2 s)]で流下するときの液膜厚さδ[m]について次元解析をおこなう。関係する物理量は重力加速度g[m/s2]を加えて5個である。液膜厚さδが次式のように表せるとする。(kは無次元の定数)
![]()
すると次元間にも次の関係が成立する。
![]()
これよりべき数間の関係式は
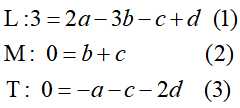
となる。 いまaを残して,他をaであらわすと, (2)より b=-c, (1)×2+(3)より c=2-a, (1)+(3)×2より d=-1なので,これより,元の関係式は次式となる。
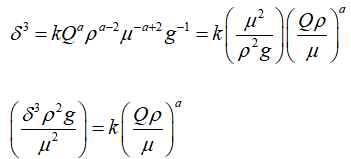
なお,この流下液膜のモデルは層流を仮定した場合は基礎式(ナビエ・ストークス式)の解析解が次式のように得られる。(放物線速度分布となる)(次元解析結果でk=3, a=1に相当する。)
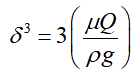
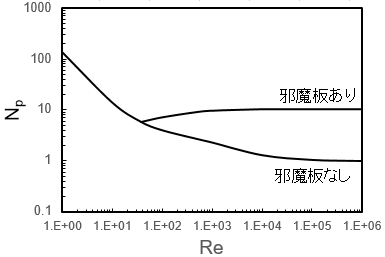
撹拌所要動力
 円筒型撹拌槽内における撹拌所要動力P [W=kg・m2/s3] に関与する物理量は,液の密度ρ
[kg/m3], 粘度μ [kg/(m・s)], 重力加速度g [m/s2], 撹拌羽根の大きさD
[m], 撹拌回転数n [1/s]である。Pに関して以下のように次元解析をおこなう。 次式の関係を仮定する。(Cは定数)
円筒型撹拌槽内における撹拌所要動力P [W=kg・m2/s3] に関与する物理量は,液の密度ρ
[kg/m3], 粘度μ [kg/(m・s)], 重力加速度g [m/s2], 撹拌羽根の大きさD
[m], 撹拌回転数n [1/s]である。Pに関して以下のように次元解析をおこなう。 次式の関係を仮定する。(Cは定数)
![]()
長さL,
質量M, 時間Tの3つの次元に関する等式が次式:
![]()
であり,これより, ![]()
a, d, e をb とc で表すと,
![]()
よって,
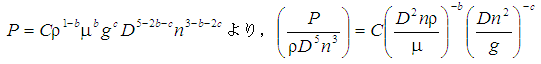
となる。得られた無次元数は順に動力数Np, 撹拌レイノルズ数Re,フルード数Frである。
ポンプの特性
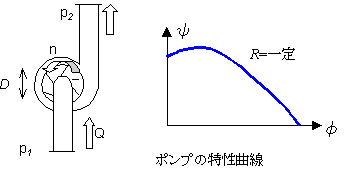 形状が相似なポンプ群は代表寸法として羽根車外径Dを指定すると大きさが決まる。その運動は軸の回転数nにより決まる。ポンプによる昇圧Δp
=p2-p1は送水量Q、流体の密度ρと粘度μが関与する。
形状が相似なポンプ群は代表寸法として羽根車外径Dを指定すると大きさが決まる。その運動は軸の回転数nにより決まる。ポンプによる昇圧Δp
=p2-p1は送水量Q、流体の密度ρと粘度μが関与する。
関与する変数物理量が6で、基本単位の数はM, L, Tの3つなので、π定理により無次元数の数は3と予測される。
各変数間の関係が、
Δp =k Q a n b D c ρd μe
とすると、次元の関係が
[ML-1T-2] =[L3T-1]a [T-1]b
[L]c [ML-3]d [ML-1T-1]
e
なので、これより、
1=d+e
1=3a+c-3d-e
2=-a-b-e
である。いまa,e を残して他をa,e
で表わすと、
b =2-a-e
d =1-e
c =2-3a-2eである。よって
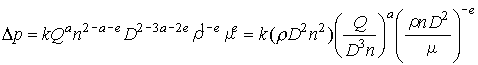
すなわち変数間の関係が、
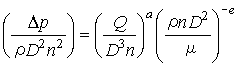
のようにグループ化される。
Ut =πdn (羽根車外周の周速度)を用いると、
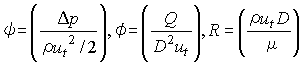
となる。ψは揚程係数、φは流量係数と呼ばれる。
ポンプの性能は大きさによらずψ-φ間の関係すなわち特性曲線によってあらわせる。特性曲線を用いるとポンプの大小、回転数にかかわりなく共通の一本の曲線で性能が示される。この原理により大小のポンプ間での性能換算が、
φ1=φ2 より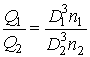
ψ1=ψ2 より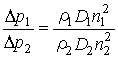 となる。
となる。
ファン(送風機)の動力
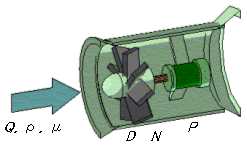 形状D[m], 回転数N[1/s]のファンにより密度ρ[kg/m3], 粘度μ[kg/(m・s)]の空気を体積流量Q[m3/s]で送風する。これに必要な動力P
[W=kg・m2/s3]について次元解析をおこなう。Pがそれらの物理量の関数であると仮定する。
形状D[m], 回転数N[1/s]のファンにより密度ρ[kg/m3], 粘度μ[kg/(m・s)]の空気を体積流量Q[m3/s]で送風する。これに必要な動力P
[W=kg・m2/s3]について次元解析をおこなう。Pがそれらの物理量の関数であると仮定する。
![]()
(kは無次元の定数)すると次元間にも次の関係が成立する。
[ML2T-3]=[ML-3]a[ML-1T-1]b[T-1]c[L]d[L3T-1]e
よって、Mに関して
![]()
Lに関して ![]()
Tに関して ![]()
bとeを残し、他をこれであらわすと、
![]()
![]()
![]()
よって、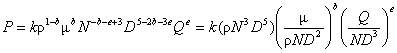
すなわち、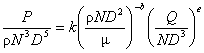 である。
である。
ここで得られた無次元数は順に動力数(power number), レイノルズ数, 流れ係数(flow coefficient)である。実用上は送風量が大きいと流れが乱流になって、粘性の効果(レイノルズ数)が無視できるため、次式が適用される。![]()
オリフィス
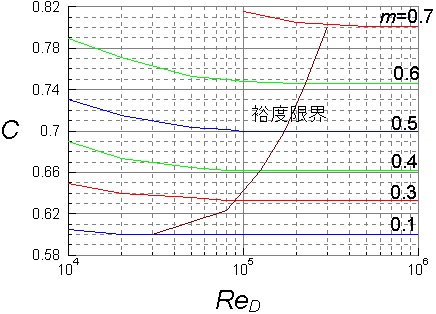
内径D の管内を密度ρ,粘度μ の流体が速度u で流れている。管内に孔径D0のオリフィス板を挿入したときのオリフィス上流・下流の圧力差ΔP [Pa=N/m2=kg/(s2-m)]について次元解析をおこなう。
関与する無次元数変数間の関係を次式のように仮定する。(Cは定数)

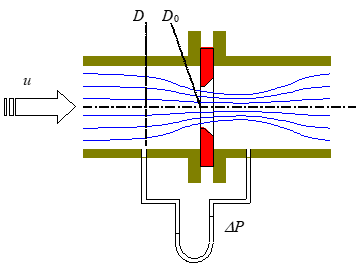
これより (2ΔP/u2ρ)=C (C:流出係数)として,Cが(Re=uρD/μ)と(D/D0)の関数(図表)として与えられる。
気泡の生成
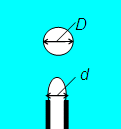 内径d
[m]のノズルから液中にガスを送入し気泡を発生させる。関係する物理量が d および液の密度ρ [kg/m3], 表面張力σ
[N/m=kg/s2], 粘度 μ [Pa・s=kg/(m・s)],重力加速度g [m/s2]であるとして,気泡径D
[m]を支配する無次元数を求める。
内径d
[m]のノズルから液中にガスを送入し気泡を発生させる。関係する物理量が d および液の密度ρ [kg/m3], 表面張力σ
[N/m=kg/s2], 粘度 μ [Pa・s=kg/(m・s)],重力加速度g [m/s2]であるとして,気泡径D
[m]を支配する無次元数を求める。
次式のような関係を仮定する。(kは無次元の定数)
![]()
すると,質量M, 長さL, 時間Tの次元間にも次の関係が成立する。
![]()
各次元についての関係は
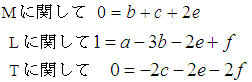
である。c とe を残し, 他をこれであらわすと
![]()
である。 これにより3つの無次元数(無次元項)が
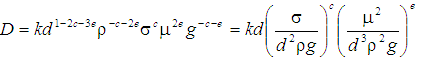
すなわち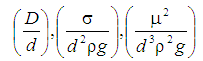 となる。
となる。
カルマン渦
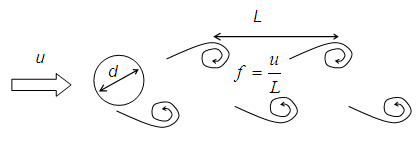 密度ρ
[kg/m3], 粘度μ [kg/(m・s)], 流速u [m/s]の流れ中に置かれた径d
[m]の円柱の後ろに,距離L [m]間隔で周期的渦(カルマン渦)が発生する。この周期 f について以下のように次元解析をおこなえ。
密度ρ
[kg/m3], 粘度μ [kg/(m・s)], 流速u [m/s]の流れ中に置かれた径d
[m]の円柱の後ろに,距離L [m]間隔で周期的渦(カルマン渦)が発生する。この周期 f について以下のように次元解析をおこなえ。
関係する物理量間に次の関係が成り立つとする。(kは定数)
![]()
これより,関係する次元すなわち,長さL,質量M,時間Tに関する等式は次式である。
![]()
各次元についての関係は

である。a ,b, d をcで表すと,![]() 。これらを式(a)に代入して整理すると,
。これらを式(a)に代入して整理すると,
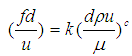 。
。
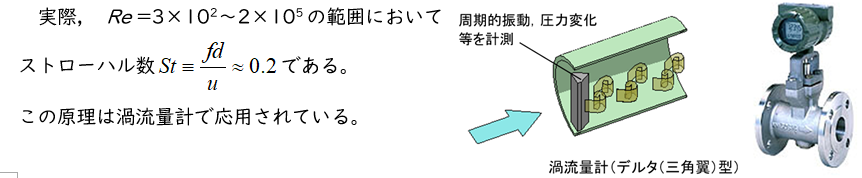
得られた無次元数は ストローハル数St とレイノルズ数Reである。
マグヌス効果
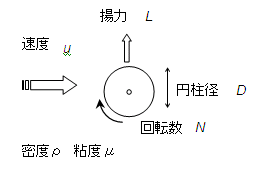 速度u
[m/s],粘性係数 μ [kg/(m-s)],密度ρ [kg/m3]の流れ中にある径D [m]の円柱が回転数 N
[1/s]で回転している。円柱におよぼされる流れに垂直な力(揚力,マグヌス効果)(単位長さあたり)L [N/m=kg/s2]について次元解析をおこなう。
速度u
[m/s],粘性係数 μ [kg/(m-s)],密度ρ [kg/m3]の流れ中にある径D [m]の円柱が回転数 N
[1/s]で回転している。円柱におよぼされる流れに垂直な力(揚力,マグヌス効果)(単位長さあたり)L [N/m=kg/s2]について次元解析をおこなう。
次式を仮定する。
![]()
次元間の関係式は次式。
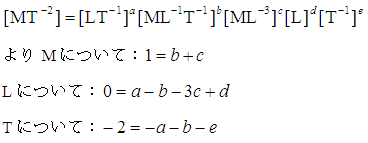
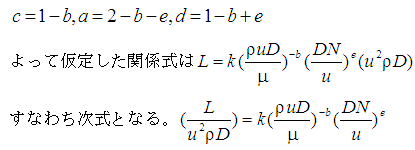
細胞の破砕機(ホモジナイザー)
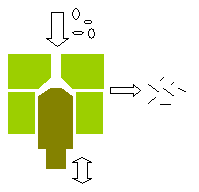 バイオプロセスにおける細胞破砕機は、シリンダ内のピストンの往復運動で機械的に細胞膜を破壊して、細胞内物質を取り出す機械である。この機械の細胞破砕処理能力は細胞破砕の時定数τ [s]、上流圧p
[Pa=kg/(s-m2)]、ピストン振動数ω [s-1]、流体密度ρ[kg/m3]、シリンダとピストンのすきま距離D
[m]の各量により支配される。
バイオプロセスにおける細胞破砕機は、シリンダ内のピストンの往復運動で機械的に細胞膜を破壊して、細胞内物質を取り出す機械である。この機械の細胞破砕処理能力は細胞破砕の時定数τ [s]、上流圧p
[Pa=kg/(s-m2)]、ピストン振動数ω [s-1]、流体密度ρ[kg/m3]、シリンダとピストンのすきま距離D
[m]の各量により支配される。
いま諸量間の関数関係が、τ=k p aωbρcD d
のようなべき関数の形であらわせるものとすると、次元に関する次式が成立する。
[M0L0T1]=[ML-1T-2]a [T-1]b
[ML-3]c [L]d
これより,Mに関して0=a+c
Lに関して 0=-a-3c+d
Tに関して 1=-2a-b
が成り立つ。いまaを残して他をaであらわすと、
c =-a,
b =-1-2a,
d =a+3c=-2a
となる。よって、
τ=k p aω-1-2aρ-aD -2a。
すなわち ![]() である。
である。
各種サイズの細胞破砕機についての実験結果はこれらの無次元数で整理され、a =2.9である。例えばD を√10倍小さくすると、圧力は1/10で同じ細胞破砕性能を持つことになる。
(参考資料:P. Belter, E.L. Cussler, W.-SS. Hu: BIOSEPARATIONS, p. 90, Wiley (1988))
対流伝熱
管径 D [m]の管内を密度ρ [kg/m3], 粘性係数μ [kg/(m・s)], 熱容量Cp [J/(kg・K) ≡ m2/(s2・K)], 熱伝導度 k [J/(s・m・K) ≡ kg・m/(s3・K)] の流体が流速 u [m/s]で流れている。流体-管壁間境膜の伝熱係数 h [kg/(s3・K)] について次元解析をおこなう。
伝熱係数が
![]()
のようにあらわせるとする。(Cは無次元の定数)すると次元間にも次の関係が成立する。(温度の次元をΘとする。)
![]()
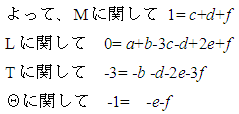
いまa
とf を残して、他をこれらであらわすと、
![]()
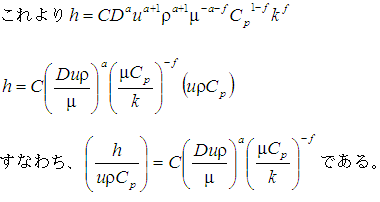
ここであらわれた無次元数は順にスタントン数St, レイノルズ数Re, プラントル数Pr である。
対流伝熱 (熱量も次元とする場合)
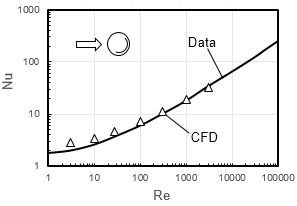
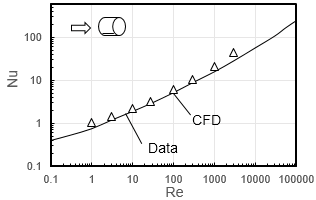
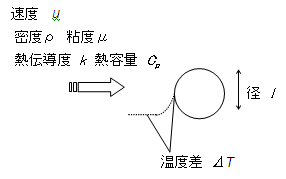 固体球から空気への強制対流伝熱速度q について以下のように次元解析をおこなう。伝熱速度q [J/(m2・s)]に関係する物理量は温度差ΔT
[K],空気の速度u [m/s],密度ρ [kg/m3],粘度μ [kg/(m-s)],熱伝導度k [J/(s・m・K)],熱容量Cp
[J/(kg・K)],固体球の径l
[m]である。これらの物理量間に次の関係が成り立つとする。(Cは定数)
固体球から空気への強制対流伝熱速度q について以下のように次元解析をおこなう。伝熱速度q [J/(m2・s)]に関係する物理量は温度差ΔT
[K],空気の速度u [m/s],密度ρ [kg/m3],粘度μ [kg/(m-s)],熱伝導度k [J/(s・m・K)],熱容量Cp
[J/(kg・K)],固体球の径l
[m]である。これらの物理量間に次の関係が成り立つとする。(Cは定数)
![]()
これより関係する次元,長さL,質量M,時間T,温度θ,熱量Hに関する等式が次式である。
![]()
これより各次元についての連立1次方程式が得られる。
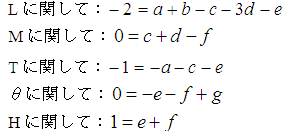
いまd
とf を残して他(a,b,c,e,g )をd,f で表すと次式となる。
![]()
よって式(1)は次式のように整理される。
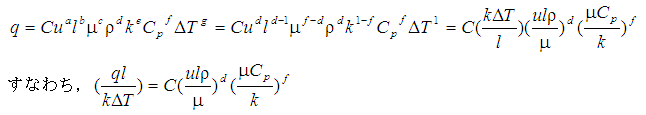
であり,順に無次元数であるヌッセルト数Nu,レイノルズ数Re,プラントル数Prがえられた。
物質移動
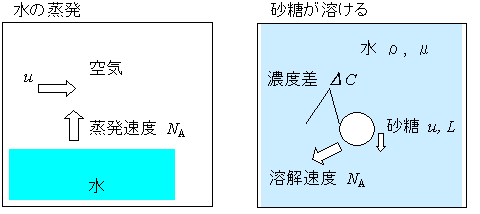 水の空気中への蒸発や砂糖の水への溶解現象は物質移動の問題である。これらの物質移動速度NA
[mol/(m2・s)]の大きさに関与する物理量は、濃度差ΔCA
[mol/m3]、拡散係数DAB
[m2/s]、速度u
[m/s]、流体の密度ρ [kg/m3]、粘性係数μ
[kg/(m・s)]、代表長さL [m]である。これらの物理量が7、次元がmol,
M, L, Tの4つであるから関係する無次元数の数は3であると予想できる。いまNAが
水の空気中への蒸発や砂糖の水への溶解現象は物質移動の問題である。これらの物質移動速度NA
[mol/(m2・s)]の大きさに関与する物理量は、濃度差ΔCA
[mol/m3]、拡散係数DAB
[m2/s]、速度u
[m/s]、流体の密度ρ [kg/m3]、粘性係数μ
[kg/(m・s)]、代表長さL [m]である。これらの物理量が7、次元がmol,
M, L, Tの4つであるから関係する無次元数の数は3であると予想できる。いまNAが
![]()
であらわせるとする。次元に関しても等式:
![]()
が成立する。よって、
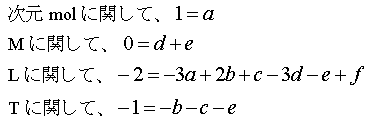
が成立する。 c とe
と残して他をこれらであらわすと、
![]()
である。よって、
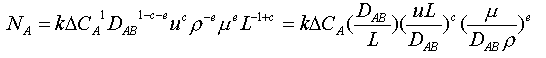
すなわち次式となる。
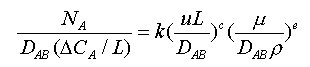
ここであらわれた3つの無次元数はそれぞれシャーウッド数
Sh, ペクレ数 Pe, シュミット数Scと呼ばれる。よって、物質移動問題は次元解析の結果より、
![]()
の形式で相関できると予想される。実際、球形固体(砂糖)の水への溶解速度は理論的に、
![]()
と予測される。ただし、Sc≫1とする。 さらに、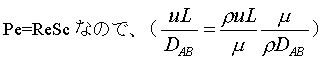 上式は、
上式は、
![]()
ともあらわせる。実際、水の蒸発(平板からの物質移動)は境界層理論から、
![]()
となる。物質移動問題はSh, Re, Scで相関されるのが普通である。
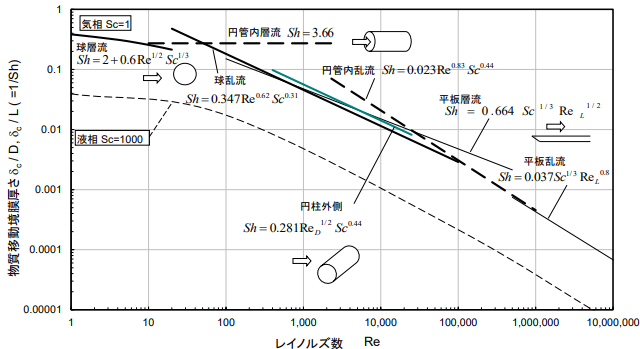
触媒有効係数
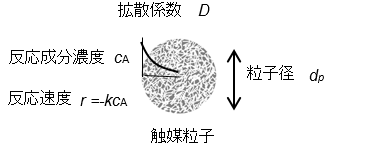
触媒粒子内で1次反応 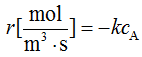 が生じている。触媒の有効係数は,
が生じている。触媒の有効係数は,
(有効係数η)=(実際の反応速度)/(理想最大反応速度)
=(反応成分平均濃度)/(表面濃度cA0で均一)
で定義される。η[-]に関与する物理量が反応速度定数 k [1/s] ,触媒粒子径 dp [m],拡散係数 D [m2/s]として,次式で表せるとする。(C1は定数。)

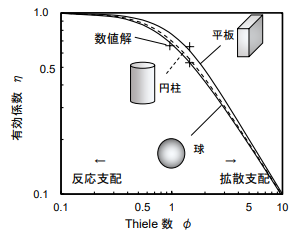
球形粒子では 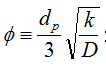 がThiele数であり,触媒有効係数ηを表すパラメーターである。
がThiele数であり,触媒有効係数ηを表すパラメーターである。
流束の比としての無次元数の定義
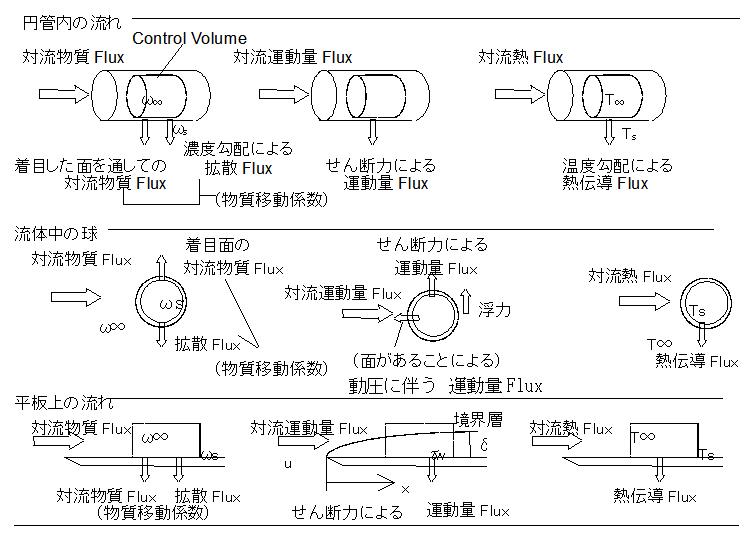
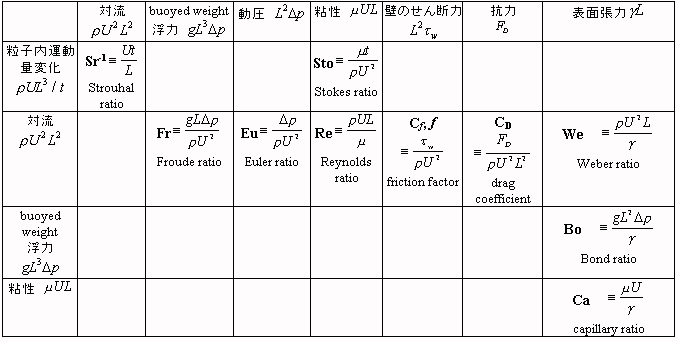
化学工学で使われる無次元数は通常「次元解析」により導かれる。しかしこれらを別の観点すなわち流束(Flux)の比としてとらえることで各無次元数の物理的意味が明確となる。
移動論では物質・熱・力(運動量)を流束(Flux)の観点から同一の方法で取り扱う。流束にはいろいろな種類があり、主なものは対流と拡散である。対流による流束は流れ自身により移動する流束である。拡散による流束 は「場」の勾配によってひきおこされる流束である。拡散の流束は物質移動の場合はFickの法則,運動量移動の場合はNewtonの法則,熱移動の場合はFourierの法則で定義される。
(移動論の視点では連続体の力学を運動量の移動としてとらえる。すなわち 力[N]=[kg・m/s2] を面を通過する運動量の流束(運動量の移動速度)[kg・m/s]*[1/s]*[1/m2]で扱う。運動量流束は力学のせん断応力および圧力と同じ次元。熱伝導の場合,温度差があると熱流束がある。これは逆にみれば温度差が定常に存在するには熱流束が必要と言える。これと同様に2面間で速度勾配が定常で存在することは面に垂直に運動量が「伝導」していることである。)
1次元の場合の単位面積あたりの各種流束とその尺度(=(m)=)
|
物質[kg] |
運動量[kg・m/s] |
熱 [kg・m2/s2](運動エネルギー) [J](熱エネルギー) |
|
対流 |
対流 |
対流 |
|
拡散(フィックの法則) |
せん断力(ニュートンの法則) |
伝導伝熱(フーリエの法則) |
|
動圧に伴う運動量流束 |
流体工学の無次元数
物質移動の無次元数

伝熱の無次元数
